Published on

Python で回転不変位相限定相関法

Authors

以前 Python で位相相関限定法 という記事を書きましたが，今回はその続きです．

位相限定相関法で XY 方向の位置ずれは算出できましたが，実利用を考えると回転とスケール(拡大縮小率)まで求めたくなります．回転角とスケールまで求める方法として，回転不変位相限定相関法(RIPOC: Rotation Invariant Phase Only Correlation)という手法が提案されており，今回はこの手法を実装してみました．

手順は以下のようになります．ポイントは Log-Polar 変換を使用して，回転とスケールを XY 方向の位置ずれに変換しているところです．

  1. 回転とスケールの算出
    1. 入力画像それぞれを FFT で変換します
    2. FFT で変換した画像それぞれに Log-Polar 変換を適用し，回転とスケールを画像の XY 方向の位置ずれに直します
    3. 位相限定相関方で XY 方向の位置ずれを算出します
    4. XY 方向の位置ずれを回転角とスケールに変換します
  2. 回転，スケールしていない画像を作成
    1. 1.で求めた回転角とスケールからアフィン変換を使用して回転，スケールしていない画像を作成します
  3. XY 方向の位置ずれを算出
    1. 回転とスケールを取り除いた画像に対して位相限定相関法を適用し，XY 方向の位置ずれを算出します

Log-Polar 変換

下記にそれぞれの画像を Log-Polar 変換した画像を載せました．比較してみると回転が Y 方向のズレ，スケールの変化が X 方向のズレに置き換えられていることがわかるかと思います．RIPOC ではこの性質をうまく利用しているようです．

lenalena_-90deglena_0.5scale
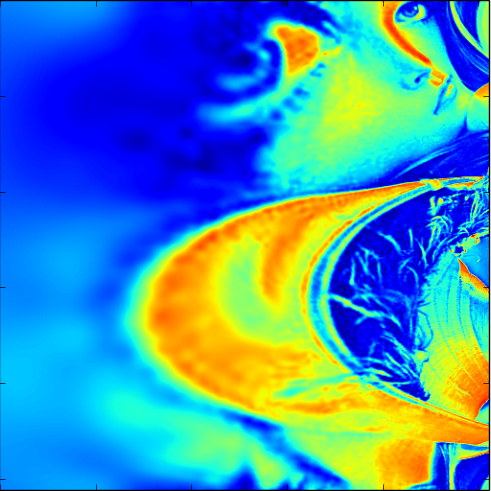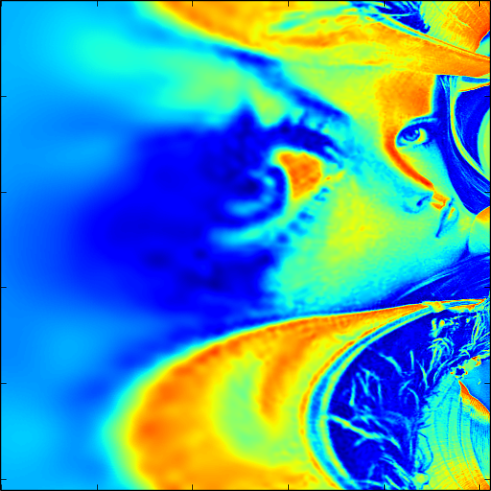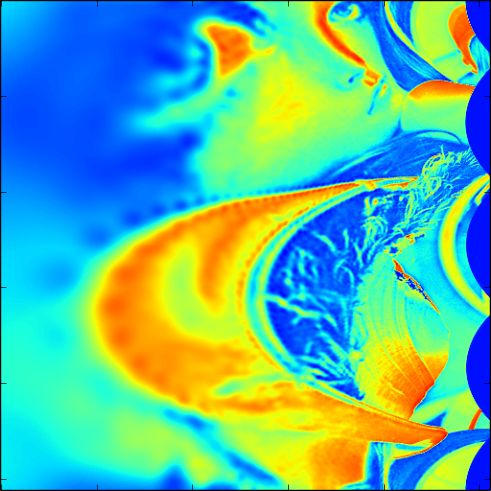lena-logpolarlena_-90deg_logpolarlena_0.5scale_logpolar

上記の画像は下記に載せた logpolar 関数を用いて生成しています．magnitude_scale = 100 として生成しました．結構この値によって，精度が左右されます．

RIPOC の Python による実装

Python による実装です．実装の資料が少なく自信がない部分があったり，画像の回転量，スケールや Log-polar 変換のパラメータによってたまに計算結果がおかしくなってしまったりしたのですが貼っておきます．

#!/usr/bin/env python
# -*- coding: utf-8 -*-
import sys

import numpy
from numpy import pi, sin, cos
from scipy.optimize import leastsq
import scipy, scipy.fftpack

import cv2
import cv2.cv as cv

import matplotlib.pyplot as plt

def logpolar(src, center, magnitude_scale = 40):

    mat1 = cv.fromarray(numpy.float64(src))
    mat2 = cv.CreateMat(src.shape[0], src.shape[1], mat1.type)

    cv.LogPolar(mat1, mat2, center, magnitude_scale, \
                cv.CV_INTER_CUBIC+cv.CV_WARP_FILL_OUTLIERS)

    return numpy.asarray(mat2)

def zero_padding(src, dstshape, pos = (0, 0)):
    y, x = pos
    dst = numpy.zeros(dstshape)
    dst[y:src.shape[0] + y, x:src.shape[1] + x] = src
    return dst

def pocfunc_model(alpha, delta1, delta2, r, u):
    N1, N2 = r.shape
    V1, V2 = map(lambda x: 2 * x + 1, u)
    return lambda n1, n2: alpha / (N1 * N2) * sin((n1 + delta1) * V1 / N1 * pi) * sin((n2 + delta2) * V2 / N2 * pi)\
                                            / (sin((n1 + delta1) * pi / N1) * sin((n2 + delta2) * pi / N2))

def pocfunc(f, g, windowfunc = numpy.hanning, withlpf = False):
    m = numpy.floor(map(lambda x: x / 2.0, f.shape))
    u = map(lambda x: x / 2.0, m)

    # hanning window
    hy = windowfunc(f.shape[0])
    hx = windowfunc(f.shape[1])
    hw = hy.reshape(hy.shape[0], 1) * hx
    f = f * hw
    g = g * hw

    # compute 2d fft
    F = scipy.fftpack.fft2(f)
    G = scipy.fftpack.fft2(g)
    G_ = numpy.conj(G)
    R = F * G_ / numpy.abs(F * G_)

    if withlpf == True:
        R = scipy.fftpack.fftshift(R)
        lpf = numpy.ones(map(lambda x: x + 1.0, m))
        lpf = zero_padding(lpf, f.shape, u)
        R = R * lpf
        R = scipy.fftpack.fftshift(R)

    return scipy.fftpack.fftshift(numpy.real(scipy.fftpack.ifft2(R)))

def poc(f, g, fitting_shape = (9, 9)):
    # compute phase-only correlation
    center = map(lambda x: x / 2.0, f.shape)
    m = numpy.floor(map(lambda x: x / 2.0, f.shape))
    u = map(lambda x: x / 2.0, m)

    r = pocfunc(f, g)

    # least-square fitting
    max_pos = numpy.argmax(r)
    peak = (max_pos / f.shape[1], max_pos % f.shape[1])
    max_peak = r[peak[0], peak[1]]

    mf = numpy.floor(map(lambda x: x / 2.0, fitting_shape))
    fitting_area = r[peak[0] - mf[0] : peak[0] + mf[0] + 1,\
                     peak[1] - mf[1] : peak[1] + mf[1] + 1]

    p0 = [0.5, -(peak[0] - m[0]) - 0.02, -(peak[1] - m[1]) - 0.02]
    y, x = numpy.mgrid[-mf[0]:mf[0] + 1, -mf[1]:mf[1] + 1]
    y = y + peak[0] - m[0]
    x = x + peak[1] - m[1]
    errorfunction = lambda p: numpy.ravel(pocfunc_model(p[0], p[1], p[2], r, u)(y, x) - fitting_area)
    plsq = leastsq(errorfunction, p0)
    return (plsq[0][0], plsq[0][1], plsq[0][2])

def ripoc(f, g, M = 50, fitting_shape = (9, 9)):

    hy = numpy.hanning(f.shape[0])
    hx = numpy.hanning(f.shape[1])
    hw = hy.reshape(hy.shape[0], 1) * hx

    ff = f * hw
    gg = g * hw

    F = scipy.fftpack.fft2(ff)
    G = scipy.fftpack.fft2(gg)

    F = scipy.fftpack.fftshift(numpy.log(numpy.abs(F)))
    G = scipy.fftpack.fftshift(numpy.log(numpy.abs(G)))

    FLP = logpolar(F, (F.shape[0] / 2, F.shape[1] / 2), M)
    GLP = logpolar(G, (G.shape[0] / 2, G.shape[1] / 2), M)

    R = poc(FLP, GLP)

    angle = -R[1] / F.shape[0] * 360
    scale = 1.0 - R[2] / 100

    center = tuple(numpy.array(g.shape) / 2)
    rot = cv2.getRotationMatrix2D(center, -angle, 1.0 + (1.0 - scale))

    g_dash = cv2.warpAffine(g, rot, (g.shape[1], g.shape[0]), flags=cv2.INTER_LANCZOS4)

    t = poc(f, g_dash)

    return (t[1], t[2], angle, scale)

シミュレーション

元画像を X 方向に 59，Y 方向に 16，7.27 度回転させた画像に RIPOC を適用してみたところ下記のようになりました．高精度に位置ずれを求められていることがわかります．

lenalena_x59_y16_7.27deg
from poc import *
img1 = cv2.imread("lena.jpg", 0)
img2 = cv2.imread("lena_x59_y16_7.27deg.jpg", 0)
ripoc(img1, img2)

(16.067704913163475,
 58.934512695463397,
 -7.2454451758682392,
 0.99979604899848151)

GitHub にも上記コードをあげています．daisukekobayashi/pocpy

Discuss on Twitter • View on GitHub