Published on

Python で最小二乗法,指数近似

Authors

最近仕事で簡単なデータ解析をしなくちゃいけないことがあります.作業は簡単で取得したデータを曲線で近似し,近似式を得るというものです.

Excel でプロットして近似式の追加で曲線の式を求めればいいだけなんですが毎回グラフを作成するのはめんどくさいし,求めた近似式を使って評価したりすることを考えると自動化したいという欲求が発生しました.

こういうとき私はだいたい Python でスクリプトを書くことが多いです.

今回は Python の Scipy の最小二乗法で近似式を求めるスクリプトを書いたのですが,Excel の近似式と数値が微妙に違うという問題に直面し半日ぐらいはまりました.そのときの覚書です.

結論から言うと指数関数のままで最小二乗法を適用していたのが問題でした.

今,近似したい式を y = a * exp( b * x ) とすると測定データ(x, y)から誤差 y = a * exp( b * x) の二乗和を最小にする(a, b)を求めるのが問題です.

このままでも解は求まるのですが, Excel は上記式の両辺に対数をとり変形し下記式の誤差を最小にする近似式を求めている模様.

log(y) = log( a * exp( b * x ) )
log(y) = ( log(a) + b * x )

Python で変形前と変形後でフィッティングし Excel と比較すると対数をとったものと Excel の近似式が同じになりました.

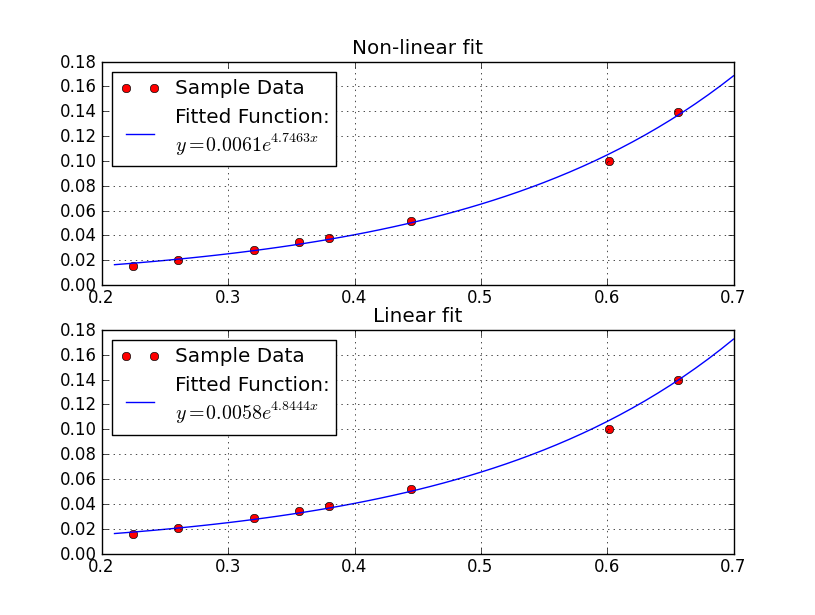
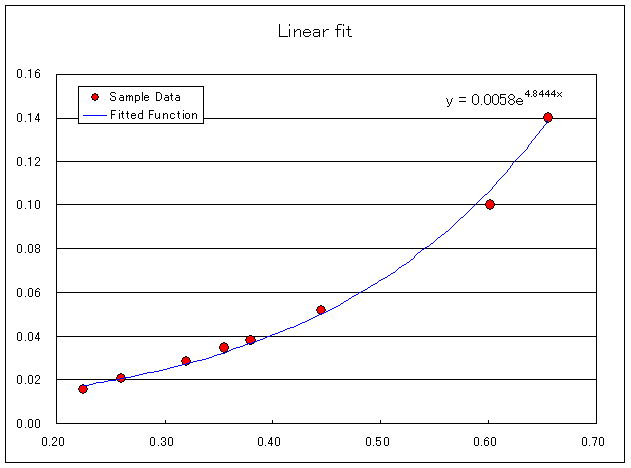
python_fitexcel_linear_fit

Python で使用したソースコードも貼っときます.

#! /usr/bin/env python
# -*- coding: utf-8 -*-

import numpy
import scipy.optimize
import matplotlib.pyplot as plt

def fit_exp(parameter, x, y):
    a = parameter[0]
    b = parameter[1]
    residual = y - (a * numpy.exp(b * x))
    return residual

def fit_exp_linear(parameter, x, y):
    a = parameter[0]
    b = parameter[1]
    residual = numpy.log(y) - (numpy.log(a) + b * x)
    return residual

def exp_string(a, b):
    return "$y = %0.4f e^{ %0.4f x}$" % (a, b)

if __name__ == "__main__":

    x = numpy.array([6.559112404564946264e-01,
                     6.013845740818111185e-01,
                     4.449591514877473397e-01,
                     3.557250387126167923e-01,
                     3.798882550532960423e-01,
                     3.206955701106445344e-01,
                     2.600880460776140990e-01,
                     2.245379618606005157e-01])

    y = numpy.array([1.397354195522357567e-01,
                     1.001406990711011247e-01,
                     5.173231204524778720e-02,
                     3.445520251689743879e-02,
                     3.801366557283047953e-02,
                     2.856782588754304408e-02,
                     2.036328213585812327e-02,
                     1.566228252276009869e-02])

    parameter0 = [1, 1]

    r1 = scipy.optimize.leastsq(fit_exp, parameter0, args=(x, y))
    r2 = scipy.optimize.leastsq(fit_exp_linear, parameter0, args=(x, y))

    model_func = lambda a, b, x: a * numpy.exp(b * x)

    fig = plt.figure()

    ax1 = fig.add_subplot(2, 1, 1)
    ax2 = fig.add_subplot(2, 1, 2)

    ax1.plot(x, y, "ro")
    ax2.plot(x, y, "ro")

    xx = numpy.arange(0.7, 0.2, -0.01)

    ax1.plot(xx, model_func(r1[0][0], r1[0][1], xx))
    ax2.plot(xx, model_func(r2[0][0], r2[0][1], xx))

    ax1.legend(("Sample Data", "Fitted Function:\n" + exp_string(r1[0][0], r1[0][1])),
                "upper left")
    ax2.legend(("Sample Data", "Fitted Function:\n" + exp_string(r2[0][0], r2[0][1])),
                "upper left")

    ax1.set_title("Non-linear fit")
    ax2.set_title("Linear fit")

    ax1.grid(True)
    ax2.grid(True)

    plt.show()

そして久しぶりに log の計算に直面し,計算の仕方とかをすっかり忘れていました.数学も勉強しないと...

Reference:

Discuss on Twitter • View on GitHub